Contenido

• Pasos
• Consejos

Los matemáticos y los programadores de gráficos a menudo necesitan encontrar el ángulo entre dos vectores. Afortunadamente, la fórmula utilizada para calcular este ángulo no requiere más que un simple producto escalar. Aunque el razonamiento detrás de esta fórmula es más fácil de entender cuando se usan vectores bidimensionales, podemos adaptarlo fácilmente a vectores con cualquier número de componentes.

Pasos

Parte 1 de 2: calcula el ángulo entre dos vectores

1. 

   Identifica los dos vectores. Escribe toda la información conocida sobre los dos vectores. A los efectos de este tutorial, asumiremos que conoce los vectores solo en términos de sus coordenadas dimensionales (también llamadas componentes). Si ya conoces el módulo o estándar de estos vectores (es decir, su longitud), puede omitir algunos de los pasos siguientes.
   • Ejemplo: consideraremos los vectores bidimensionales = (2,2) y = (0,3). Estos dos vectores se pueden reescribir como = 2yo + 2j e = 0yo + 3j = 3j.
   • Aunque nuestro ejemplo usa dos vectores bidimensionales, podemos aplicar las siguientes instrucciones a vectores con cualquier número de componentes.

2. 

   
   
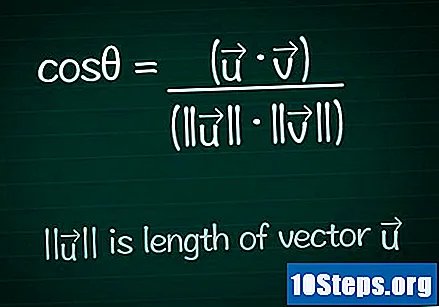
   Escribe la fórmula del coseno. Para encontrar el valor del ángulo θ entre dos vectores cualesquiera, primero debemos calcular el coseno de ese ángulo. Puede buscar y encontrar la fórmula en detalle o simplemente escribirla como se muestra a continuación:
   • cosθ = (•) / (|||| ||||)
   • |||| representa el módulo (o longitud) del vector ".
   • • representa el producto escalar (o producto interno) de los dos vectores.

3. 

   
   
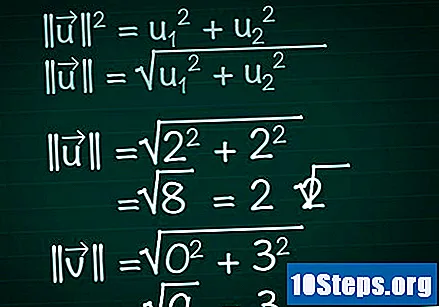
   Calcula el módulo de cada vector. Imagina un triángulo rectángulo formado por el componente X de un vector, su componente y y el vector en sí. En este triángulo, el vector juega el papel de hipotenusa; por lo tanto, para encontrar su longitud, aplicaremos el teorema de Pitágoras. Como resultado, esta fórmula es fácilmente aplicable a vectores con cualquier número de componentes.
   • || u || = u₁ + u₂. Si el vector tiene más de dos componentes, simplemente continúe agregando + u₃ + u₄ +...
   • Por lo tanto, para un vector bidimensional, tendremos que || u || = √ (u₁ + u₂).
   • En nuestro ejemplo, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Calcula el producto escalar entre los dos vectores. Ya debería conocer el método para multiplicar vectores, también llamado producto escalar. Para calcular el producto escalar de dos vectores en términos de sus componentes, multiplicamos los componentes en la misma dirección entre sí y luego sumamos los resultados de esos productos.
   • Si trabaja con programas de gráficos por computadora, primero visite la sección "Sugerencias" antes de continuar.
   • En términos matemáticos, • = u₁v₁ + u₂v₂, donde u = (u₁, u₂). Si su vector tiene más de dos componentes, simplemente continúe agregando + u₃v₃ + u₄v₄...
   • En nuestro ejemplo, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Este es el valor del producto escalar entre los vectores y.

5. 

   Sustituye estos resultados en la fórmula del coseno. Recuerde, cosθ = (•) / (|||| || ||). Ya hemos calculado el producto escalar y el módulo de los dos vectores. Ahora, reemplacemos estos valores en la fórmula y calculemos el coseno del ángulo.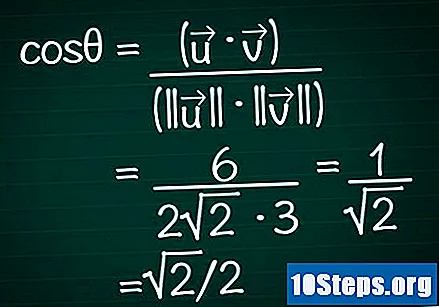
   • En nuestro ejemplo, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Encuentra el ángulo según tu coseno.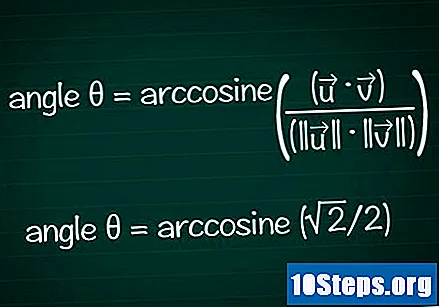
   Usa la función de arco o cos de tu calculadora para determinar el ángulo θ a partir de tu valor de coseno. En algunos casos, es posible que pueda encontrar el valor del ángulo basándose en el círculo unitario.
   • En nuestro ejemplo, cosθ = √2 / 2. Escribe "arccos (√2 ​​/ 2)" en tu calculadora para encontrar el ángulo. Otra opción es buscar el ángulo θ del círculo unitario donde cosθ = √2 / 2: esto será cierto para θ = /₄ o 45 °.
   • Juntando toda la información, tendremos la fórmula final θ = arcocoseno ((•) / (|||| || ||))

Parte 2 de 2: Definición de la fórmula para calcular el ángulo

1. 

   Comprende el propósito de la fórmula. La fórmula que usamos para calcular el ángulo entre dos vectores no se derivó de reglas preexistentes; en cambio, se creó como una definición del producto escalar entre dos vectores y el ángulo entre ellos. Sin embargo, esta decisión no es arbitraria. Con una mirada más cercana a la geometría básica, podemos ver por qué esta fórmula da como resultado definiciones tan útiles e intuitivas.
   • Los siguientes ejemplos utilizan vectores bidimensionales porque son el tipo más intuitivo para trabajar. Los vectores de tres o más dimensiones tienen sus propiedades definidas a partir de la fórmula general (también de forma muy similar).

2. 

   Repase la ley del coseno. En cualquier triángulo, considere el ángulo θ formado por los lados los y si y el lado C opuesto a ese ángulo. Según la ley del coseno, c = a + b -2abpretina(θ). La demostración de esta fórmula se puede obtener fácilmente a partir del conocimiento de la geometría básica.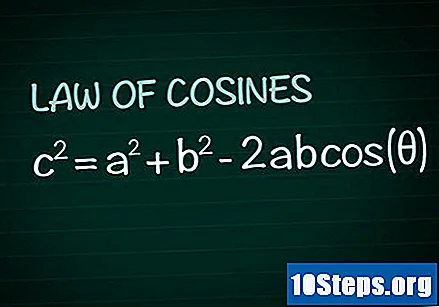

3. 

   Conecta los dos vectores para formar un triángulo. Dibuja un par de vectores y, con un ángulo θ entre ellos. Luego, dibuja un tercer vector entre ellos para formar un triángulo. En otras palabras, dibuje el vector tal que + =, o simplemente = -.

4. 

   Aplica la ley del coseno a este triángulo. Reemplace la longitud de los lados de nuestro triángulo de vector (es decir, el módulo del vector) en la fórmula de la ley del coseno:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||pretina(θ)

5. 

   Reescribe la fórmula usando productos escalares. Recuerde que el producto escalar es la ampliación de un vector proyectado sobre otro. El producto escalar de un vector en sí mismo no requiere proyección porque no hay cambio de dirección. Esto significa que • = || a ||. Con base en esta información, reescribamos la ecuación de la ley del coseno:
   • (-) • (-) = • + • - 2 || a || || b ||pretina(θ)

6. 

   Simplifica la fórmula. Expande los productos en el lado izquierdo de la ecuación y luego simplifícalos hasta que alcances la fórmula que conocemos para calcular ángulos.
   • • - • - • + • = • + • - 2 || a || || b ||pretina(θ)
   • - • - • = -2 || a || || b ||pretina(θ)
   • -2 (•) = -2 || a || || b ||pretina(θ)
   • • = || a || || b ||pretina(θ)

Consejos

• Para una resolución rápida, aplique la siguiente fórmula a cualquier par de vectores bidimensionales: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Si trabaja con programas de gráficos por computadora, lo más probable es que solo necesite conocer la dirección de los vectores, no su longitud. Siga los pasos a continuación para simplificar las ecuaciones y acelerar su programa:
  • Normalice cada vector, es decir, encuentre el vector unitario que tiene la misma dirección que el vector original. Para hacer esto, divida cada componente del vector por el módulo de vector.
  • Calcule el producto escalar de los vectores normalizados, no los vectores originales.
  • Dado que el módulo (es decir, la longitud) de los vectores normalizados es unitario, podemos dejarlos fuera de la fórmula. Su ecuación final para calcular ángulos será arcos (•).
• Con base en la fórmula de la ley del coseno, podemos averiguar rápidamente si el ángulo en cuestión es agudo u obtuso. Comience con cosθ = (•) / (|||| ||||):
  • Los lados izquierdo y derecho de la ecuación deben tener el mismo signo (positivo o negativo).
  • Como las longitudes son siempre positivas, cosθ siempre tendrá el mismo signo que el producto escalar.
  • Por tanto, si el producto escalar es positivo, cosθ será positivo. Esto significa que el ángulo está en el primer cuadrante del círculo unitario, es decir, θ <π / 2 o 90 °. Por tanto, el ángulo es agudo.
  • Si el producto escalar es negativo, cosθ es negativo. Esto significa que el ángulo está en el segundo cuadrante del círculo unitario, es decir, π / 2 <θ ≤ π o 90 ° <θ ≤ 180 °. Por tanto, el ángulo es obtuso.